Great question! In order for two Lego Technic gears to mesh their teeth spacing must be the same - therefore all Lego gears (that mesh) have the same teeth spacing. Now you can think of a gear as a circle with a number of teeth fitted around the outside (imagine a string of teeth wrapped around a circle) and therefore the number of teeth that fit around the circle is just the circumference of the circle divided by the width of the teeth. Of course in order for two gears to mesh and drive each other the teeth have to overlap between the gears as shown in the diagram below. The red circles are known as the pitch circles representing the distance from the center of each gear such that the pitch circles of meshing gears touch. The pitch circles have a pitch radius of r which is also sometimes described by a pitch diameter. In the case of same sized gears that means the pitch circles are the same size and the distance between the centers of the gears is simply 2r (two times the radius of the pitch circle) or simply the pitch diameter.

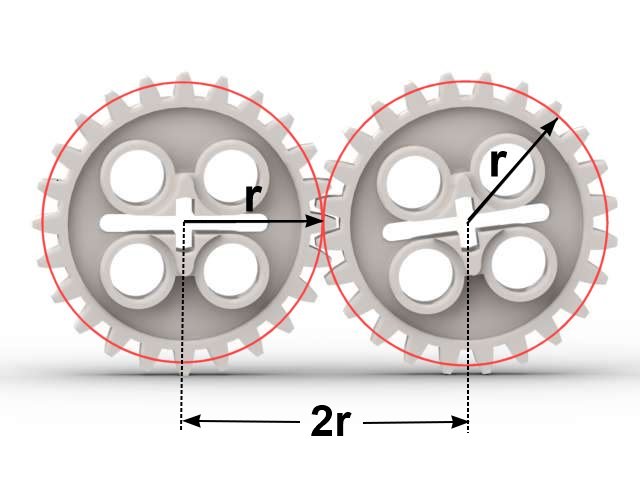
Now the circumference of a circle is related to the radius of the circle by the well known formula 2 x pi x r where r is the radius of the circle. Since this is a linear relationship it means that if for example you double the radius of a gear then the number of teeth around it will double as well.  So a 40 tooth gear will have two times the radius of a 20 tooth gear.

When the Lego company first designed the Lego gears they had to choose a tooth sizing that would work well and they decided to choose a sizing such that:

Pitch Radius = Gear Teeth / 16 (in Lego units)

So to work out the pitch radius of a gear you just divide the number of teeth on the gear by 16. So for example a 24 tooth gear has a pitch radius of 24 / 16 = 1.5.

Since almost all Lego Gears have teeth with multiples of 4 it means that the pitch radius of most gears are multiples of 0.25 (1/4), e.g. 1.25, 1.5, 1.75, 2.0, 2.25 etc.

What makes the pitch radius important is that the distance between the centers (or axles) of two meshing gears is simply the sum of the pitch radii of the two gears and it is this fact allows you to work out the required distance between any two gears in order to mesh them correctly. The equation is:

axle spacing = r1 + r2

where r1 and r2 are the pitch radii of the gear 1 and gear 2 respectively. Combining this equation with the one above gives:

axle spacing = (t1 + t2) / 16

where t1 and t2 are the number of teeth on gear 1 and gear 2.

For example consider the following common Lego Technic meshing of a 12 tooth gear driving a 20 tooth gear:

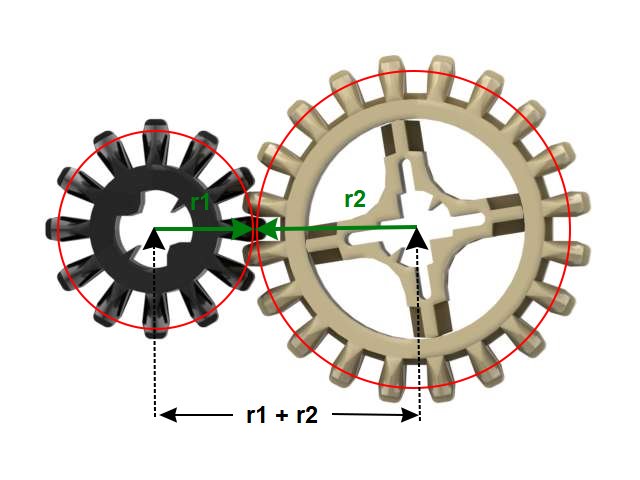
We have t1 = 12 and t2 = 20, therefore the axle spacing is (12 + 20) / 16 = 2 which is simply a spacing of two units on a liftarm. Now generally it is not easy or convenient to create fractional spacing, e.g. 1.5 or or 1.75 so to easily mesh two gears on a regular spacing the sum of their teeth must be a multiple of 16. Some the well known combinations are 8 + 8,  8 + 24, 16 + 16, 12 + 20,  24 + 24, 20 + 28, 12 + 36, 8 + 40, 28 + 36, 24 + 40, 8 + 56. To mesh other combinations of gears more advanced techniques are required.